I. Présentation du puzzle▲
Le kuromasu est un puzzle logique inventé par la société Nikoli.
Il est joué sur une grille rectangulaire composée de cases blanches ou noires. Au départ, toutes les cases sont blanches et certaines contiennent des nombres. Ces nombres représentent le total de cases blanches visibles de la case où figure le nombre dans les quatre directions, le total inclut la case elle-même.
La résolution consiste à ajouter des cases noires sur la grille en respectant deux règles :
- deux cases noires ne peuvent pas être adjacentes (avoir un côté commun, mais elles peuvent avoir un sommet commun) ;
- toutes les cases blanches doivent être connectées les unes aux autres par un chemin horizontal/vertical composé d'autres cases blanches.
Plus de renseignements sur ce puzzle peuvent être obtenus ici.
II. Pourquoi utiliser une bibliothèque de programmation logique par contraintes ?▲
Ce type de puzzle se prête bien à une résolution par contraintes, le domaine des couleurs possibles des cases est restreint (blanc/noir) et les règles sont facilement exprimables en termes de contraintes.
L'intérêt de la bibliothèque de contraintes est qu'on ne donne pas d'algorithme de résolution, on se contente de coder les règles du puzzle et c'est tout, le programme se débrouille tout seul.
Plus de renseignements sur la bibliothèque de programmation par contraintes de SWI-Prolog écrite par Markus TriskaLa home page de Markus Triska peuvent être obtenus ici.
On utilisera 0 et 1 pour coder la couleur des cases. Il « paraît logique », d'après l'énoncé des règles, que le blanc soit codé 1 et le noir 0.
La grille est représentée par une simple liste.
Les données sont codées sous la forme d'une liste de triplets case(Lig, Col, Nombre)
L'appel au prédicat de résolution de la grille est de la forme kuromasu(+Hauteur, +Largeur, ?Contraintes, ?Solution, +Options) où Hauteur est le nombre de lignes de la grille, Largeur le nombre de cases d'une ligne, Contraintes la liste des contraintes sur le nombre de cases visibles, Solution la liste obtenue en retour d'appel du prédicat, Options, une liste d'options pour la phase de recherche des solutions, ce point est détaillé dans un chapitre spécial.
Comme on peut le voir sur la signature du prédicat, Contraintes et Solution sont précédées du « ? » ce qui signifie que le prédicat fonctionne dans les deux sens, si on fournit une liste de contraintes, il fournit une grille solution mais, si on lui fournit une solution, il est capable de fabriquer une liste de contraintes.
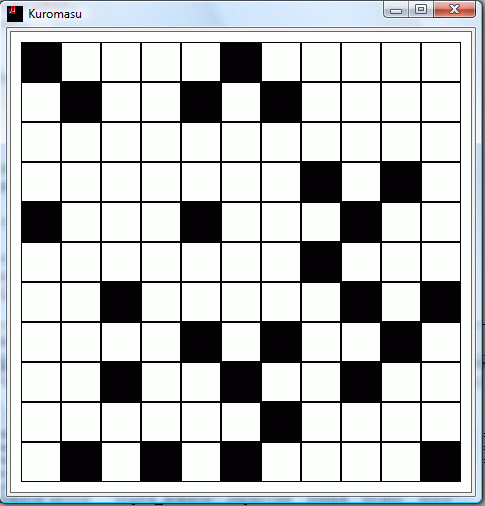
Cette liste Solution sera affichée dans une fenêtre. Voici le résultat obtenu pour le Kuromasu proposé sur le site précédent.
III. Le module de résolution des Kuromasu▲
Ce module sera appelé aussi bien dans le cadre du calcul d'une grille (la liste des contraintes étant fournie) que dans le cadre du calcul des contraintes (la grille solution étant fournie).
III-A. Le prédicat de résolution▲
Il a pour fonction de mettre en accord la grille avec la liste des contraintes. Elle se fait en deux temps :
- le codage des contraintes ;
- aa recherche effective des solutions.
On commence par traiter la liste des contraintes. Puis, comme rien n'assure que toutes les cases de la grille soient initialisées par les contraintes, les cases non initialisées seront colorées en blanc. On s'assure ensuite que toutes les cases blanches sont connectées (aucune n'est entièrement entourée de cases noires).
Enfin la recherche effective des solutions se fait en demandant le « labeling » : prédicat de la bibliothèque des contraintes.
Les contraintes étant données sous la forme d'une liste de triplets case(Lig, Col, Nombre) indépendants les uns des autres, un traitement par maplist/2 s'impose (/2 car il n'y a pas de résultat attendu au traitement). La liste Solution, ainsi que ses dimensions sont nécessaires au prédicat de traitement, on aura donc un appel par maplist(conditions(Solution, Hauteur, Largeur), Donnees). Le prédicat de traitement des contraintes doit effectuer trois tâches :
- initialiser la case concernée à 1, c'est une case blanche ;
- imposer une contrainte sur le nombre de cases blanches visibles dans les quatre directions ;
- s'assurer que les trois cases adjacentes à la case noire ajoutée pour clore un alignement, si l'on n'est pas en fin de rangée, sont blanches.
III-B. La contrainte sur le nombre de cases blanches▲
Le code de ce prédicat est :
conditions(Solution, Hauteur, Largeur, case(L, C, N)) :-
% Calcul de la position de la case dans la liste
P #= Largeur * L + C,
% Affectation de la valeur 1 à cette case.
nth0(P, Solution, 1),
% On fait la somme des nombres sur la ligne et la colonne
% autour de la case. Cette somme est égale à N-1
ValMax #= N - 1,
V1 #= 0,
C1 #= C - 1,
somme_ligne_gauche(Solution, Hauteur, Largeur, L, C1, V1, Val1, ValMax),
L1 #= L - 1,
ValMax1 #= ValMax - Val1,
ValMax1 #>= 0,
somme_colonne_haut(Solution, Hauteur, Largeur, L1, C, V1, Val2, ValMax1),
ValMax2 #= ValMax1 - Val2,
ValMax2 #>= 0,
C2 #= C + 1,
somme_ligne_droite(Solution, Hauteur, Largeur, L, C2, V1, Val3, ValMax2),
ValMax3 #= ValMax2 - Val3,
ValMax3 #>= 0,
L2 #= L+1,
somme_colonne_bas(Solution, Hauteur, Largeur, L2, C, V1, Val4, ValMax3),
Val1+Val2+Val3+Val4 #= ValMax.L'affectation d'une contrainte de visibilité de cases blanches doit prendre en compte tous les cas possibles et donc il faut connaître le nombre total de cases visibles dans les quatre directions. La somme de ces nombres doit être égale à N - 1.
Pour optimiser le calcul, on indique la valeur maximale que peut prendre le nombre à chaque étape de celui-ci. Le #= impose la contrainte que la somme Val1+Val2+Val3+Val4 soit égale à N1. On ne détaillera que le code de somme_ligne_gauche/8, les trois autres prédicats fonctionnant de manière similaire.
L'appel se fait par somme_ligne_gauche(Solution, Hauteur, Largeur, L, C1, V1, Val1, ValMax). Le prédicat s'écrit somme_ligne_gauche(Solution, Hauteur, Largeur, L, C, Val, ValF, ValMax). Détaillons les arguments d'appel :
- Solution : la liste solution dont les éléments sont modifiés ;
- Hauteur : le nombre de cases d'une colonne de la grille ;
- Largeur : le nombre de cases d'une ligne de la grille ;
- L : la ligne courante en traitement ;
- C : le numéro de case de démarrage de la recherche sur la gauche.
- Val : le nombre « courant » de cases blanches à gauche à l'appel du prédicat ;
- ValF : le nombre total de cases blanches à gauche de la case d'appel du prédicat ;
- ValMax : le nombre maximal de cases blanches à gauche de la case d'appel du prédicat.
L'appel de ce prédicat s'arrête pour trois raisons :
- on a dépassé le bord de la ligne (C a la valeur -1) ;
- on a atteint le maximum possible de cases visibles (on pose alors une case noire) ;
- la case courante est une case noire (elle a la valeur 0).
Lorsque la case courante est blanche, on augmente de 1 l'accumulateur Val, et on passe à la case directement à gauche de celle étudiée. Nous obtenons le code suivant :
% on rencontre une case blanche on continue
somme_ligne_gauche(Solution, Hauteur, Largeur, L, C, Val, ValF, ValMax) :-
C #> -1,
Val #< ValMax,
P #= Largeur * L + C,
nth0(P, Solution, 1),
Val1 #= Val + 1,
C1 #= C-1,
somme_ligne_gauche(Solution, Hauteur, Largeur, L, C1, Val1, ValF, ValMax).
% ici on rencontre une case noire, ou on en pose une
% on arrête et on s'assure que les cases adjacentes sont blanches
somme_ligne_gauche(Solution, Hauteur, Largeur, L, C, ValF, ValF, ValMax) :-
C #> -1,
ValF #< ValMax,
P #= Largeur * L + C,
nth0(P, Solution, 0),
case_haut_blanc(Solution, Largeur, L, C),
case_gauche_blanc(Solution, Largeur, L, C),
case_bas_blanc(Solution, Hauteur, Largeur, L, C).
% ici on a atteint le maximum possible
% on met la case en noir et on force les cases adjacentes à blanc
somme_ligne_gauche(Solution, Hauteur, Largeur, L, C, ValMax, ValMax, ValMax) :-
C #> -1,
P #= Largeur * L + C,
nth0(P, Solution, 0),
% on vient de la droite, on force les cases adjacentes à blanc
case_haut_blanc(Solution, Largeur, L, C),
case_gauche_blanc(Solution, Largeur, L, C),
case_bas_blanc(Solution, Hauteur, Largeur, L, C).
% ici on sort donc on arrête
somme_ligne_gauche(_Solution, _Hauteur, _Largeur, _L, C, ValF, ValF, _ValMax) :-
C #=< -1.Il vaut mieux effectuer les tests C > -1 et C =< -1, qui sont plus lisibles que l'usage du cut (!).
Le code pour forcer une case donnée en blanc est très simple, l'exemple donné correspond à la coloration de la case au-dessus de la case courante :
% On est sur la case (L, C), on regarde celle du dessus (L-1, C)
case_haut_blanc(_Solution, _Largeur, 0, _C).
case_haut_blanc(Solution, Largeur, L, C) :-
L #> 0,
P #= (L-1) * Largeur + C,
nth0(P, Solution, 1).III-C. La contrainte sur la connexité des cases blanches▲
Pour s'assurer que toutes les cases blanches sont accessibles les unes aux autres, on va parcourir les cases blanches de la grille initiale à partir de la première (ou la deuxième si la première est noire) case et en mémorisant notre passage dans une liste annexe. Une fois ce parcours terminé, on noircira les cases non visitées de la liste annexe puis on vérifiera que toutes les cases blanches ont bien été parcourues en calculant les sommes de tous les nombres des deux listes et en comparant les deux sommes obtenues.
Le calcul des sommes des listes se fait avec le prédicat de la librairie de contraintes sum/3 dont la signature est sum(+Vars, +Rel, +Expr) et dont voici le texte de documentation :
sum(+Vars, +Rel, +Expr)
The sum of elements of the list Vars is in relation Rel to Expr.
La somme des éléments de la liste Vars est en relation Rel avec l'évaluation de l'expression Expr
For example:
?- [A,B,C] ins 0..sup, sum([A,B,C], #=, 100).
A in 0..100,
A+B+C#=100,
B in 0..100,
C in 0..100.L'appel est explore_grille(Solution, Hauteur, Largeur, L).
Étant donné que la première case peut être noire ou blanche, il faut deux clauses pour écrire le prédicat.
% Parcours des cases blanches
% On est sûr qu'il n'y a pas deux cases noires consécutives
explore_grille([1 | T], Hauteur, Largeur, [1 |L ]) :-
explore([1 | T], Hauteur, Largeur, [1 | L], 0, 0).
explore_grille([0 | T], Hauteur, Largeur, [0 | L]) :-
explore([0 | T], Hauteur, Largeur, [0 | L], 0, 1).On est assuré d'être sur une case blanche lorsque l'appel à explore/6 se fait.
L'exploration d'une case consiste à étudier les quatre cases adjacentes.
Le prédicat s'écrit :
% ici la case courante est un 1
explore(Src, Hauteur, Largeur, But, L, C) :-
% on explore dans les 4 directions,
explore_haut(Src, Hauteur, Largeur, But, L, C),
explore_droite(Src, Hauteur, Largeur, But, L, C),
explore_bas(Src, Hauteur, Largeur, But, L, C),
explore_gauche(Src, Hauteur, Largeur, But, L, C).Pour l'étude d'une case, quatre cas peuvent se présenter :
- la case n'existe pas, car on teste une case hors de la grille, on s'arrête ;
- la case a déjà été visitée, on s'arrête ;
- la case n'a pas encore été visitée, elle est noire, on mémorise qu'elle a été visitée et on s'arrête ;
- la case n'a pas encore été visitée, elle est blanche, on mémorise qu'elle a été visitée, on la visite, et donc on recommence l'exploration.
On teste qu'une case n'a pas été visitée en regardant si la valeur correspondante V1, obtenue par nth0(P, But, V1) est une variable libre ou non, le prédicat utilisé est var/1 qui réussit si V1 est libre c'est-à-dire n'a pas encore été unifiée. On ne détaillera que le prédicat explore_haut/6.
% ici la case courante est blanche,
% la case correspondante de la liste annexe est libre, donc on la marque
% on continue notre exploration
explore_haut(Src, Hauteur, Largeur, But, L, C) :-
L1 #= L - 1,
L1 #> -1,
P #= L1 * Largeur + C,
nth0(P, Src, 1),
nth0(P, But, V1),
% si V1 est libre, c'est la première fois qu' on passe
var(V1),
V1 #= 1,
explore(Src, Hauteur, Largeur, But, L1, C).
explore_haut(_Src, _Hauteur, Largeur, But, L, C) :-
L1 #= L - 1,
L1 #> -1,
P #= L1 * Largeur + C,
nth0(P, But, V1),
% si V1 est libre, c'est la première fois qu' on passe
nonvar(V1).
explore_haut(Src, _Hauteur, Largeur, But, L, C) :-
L1 #= L - 1,
L1 #> -1,
P #= L1 * Largeur + C,
nth0(P, Src, 0),
nth0(P, But, V1),
% si V1 est libre, c'est la première fois qu' on passe
var(V1),
V1 #= 0 .
explore_haut(_Src, _Hauteur, _Largeur, _But, L, _C):-
L #=< 0.III-D. Lancement de la recherche des solutions▲
Il se fait tout simplement par le prédicat labeling(Options, Solution).
% obtention des solutions
solve(Options, Solution) :-
labeling(Options, Solution).Conseil de Markus TriskaLa home page de Markus Triska
Le problème de la terminaison est crucial dans la programmation logique par contraintes.
Il vaut mieux séparer la phase de déclaration du problème de la phase de « labeling ». Cela permet de vérifier que la description du problème a été bien faite, et que lorsqu'on lancera la résolution du Kuromasu celle-ci s'arrêtera. Le « labeling » calcule TOUTES les solutions et il est GARANTI de s'arrêter. Si la déclaration du problème amène à une configuration qui s'arrête, alors le calcul des solutions s'arrêtera.
Par exemple, dans le cas des Kuromasu, pour vérifier ceci, on commente la ligne solve(Options, Solution) et on lance en ligne de commande :
grille96(Hauteur, Largeur, Conditions), kuromasu(Hauteur, Largeur, Conditions, Soluce, []), false.
La recherche ne doit donner qu'une solution.
III-E. Le code complet du prédicat de résolution des Kuromasu▲
% Donnees est la liste des conditions énoncées sous la forme
% case(Lig, Col, N),
% N étant le nombre des cases blanches adjacentes (y compris cette case)
% Solution est la grille solution
kuromasu(Hauteur, Largeur, Donnees, Solution, Options)
% L sera utilisée pour la recherche de connexité des cases blanches
Len #= Hauteur * Largeur,
length(L, Len),
% les cases ont deux valeurs possibles
% noires -> 0
% blanches -> 1
Solution ins 0..1,
% Etude des données
% on fixe les visibilités des cases blanches déclarées et
% on s'assure que lorsqu'on place une case noire,
% les autres cases adjacentes ne sont pas noires
maplist(conditions(Solution, Hauteur, Largeur), Donnees),
% ici les contraintes de visibilité des cases blanches
% et de non-connexité des cases noires sont respectées
% S'il reste des cellules libres elles doivent être blanchies (valeur 1)
maplist(colorie(1), Solution),
% On vérifie maintenant que toutes les cellules blanches sont connectées
explore_grille(Solution, Hauteur, Largeur, L),
% Il faut que toutes les variables libres de L soient noircies (valeur 0)
maplist(colorie(0),L),
% le total des cases blanches doit être identique dans les deux listes
sum(L, #=, TT),
sum(Solution, #=, TT),
solve(Options, Solution).On retrouve bien la philosophie Prolog, on déclare des faits (les données sur la visibilité de certaines cases blanches), on donne des règles (deux cellules adjacentes ne peuvent être noires, et toutes les cases blanches sont connectées) et à partir de là, on interroge Prolog : solve(Options, Solution).
IV. L'affichage du Kuromasu▲
Cet affichage se fait dans une fenêtre dont on calcule les dimensions. On affiche la grille case par case, dès qu'on a affiché une ligne complète, on passe au début de la ligne suivante.
Le code se trouve dans le fichier « affiche-kuromasu.pl ». Cet affichage ne présente pas de difficulté particulière :
affiche_solution(Hauteur, Largeur, Solution) :-
% création de la fenêtre d'affichage avec son titre
new(D, window('Kuromasu')),
% calcul des dimensions
DX is Largeur * 40 + 20,
DY is Hauteur * 40 + 20,
% affectation de la taille à la fenêtre
send(D, size, new(_, size(DX,DY))),
% affichage de la fenêtre
send(D, open),
% affichage de la grille proprement dit
affiche_solution(D, Solution, Largeur, 0, 0).
%affiche_solution(Fenetre,
% Solution,
% Largeur,
% LigneCourante,
% CaseCourante)
% ici il n'y a plus rien à afficher, on s'arrête.
affiche_solution(_D, [], _, _, _) :- !.
% lorsqu'on a terminé d'afficher une ligne
affiche_solution(D, Solution, Largeur, L, Largeur) :-
% on passe à la ligne suivante.
L1 is L+1,
affiche_solution(D, Solution, Largeur, L1, 0).
% on affiche la case H
affiche_solution(D, [H | T], Largeur, L, C) :-
% on crée un carré blanc de 40 pixels sur 40
new(B, box(40,40)),
% on le colorie en noir ou on le laisse intact
( H = 0, send(B, fill_pattern, colour(@default, 0, 0, 0)); true),
% on calcule sa position d'affichage dans la fenêtre
X is 40 * C + 10,
Y is 40 * L + 10,
% et on dit à la fenêtre de l'afficher
send(D, display, B, point(X,Y)),
% on passe à la case suivante
C1 is C+1,
affiche_solution(D, T, Largeur, L, C1).V. La recherche d'une grille à partir des contraintes▲
Deux programmes sont proposés, un programme console qui calcule la grille à partir d'une liste de contraintes codée à la main (fichier « solve_console.pl ») et un programme graphique écrit en XPCE qui permet de saisir directement les contraintes dans les cases d'une grille (fichier « solve-XPCE.pl »).
L'interface XPCE dans « solve-XPCE.pl » comprend un module utilisant une version modifiée du source Prolog « editable_text.pl ». La modification a été faite pour permettre à l'utilisateur d'être averti s'il n'a pas validé sa saisie par ENTER dans une case. Voir le code sourceLe source du fichier editable_text.pl du fichier pour les détails.
Une partie du code de « solve_console.pl » est donnée ici, il est complété par l'énoncé des contraintes concernant différentes grilles préprogrammées.
:- use_module(library(clpfd)).
solve_console :-
% 11 X 11 --> 15 494 026 inférences, 3.41 CPU
% grille_1(Hauteur, Largeur, Conditions),
% 9 X 9 --> 52 952 inférences, 0.02 CPU
% grille_2(Hauteur, Largeur, Conditions),
% 10 X 10 --> 3 416 987 inférences, 0.72 CPU
% grille_3(Hauteur, Largeur, Conditions),
% 15 X 15 --> 1 798 447 inférences, 0.34 CPU
% grille_4(Hauteur, Largeur, Conditions),
% 13 X 13 --> 628 443 inférences, 0.14 CPU
% grille96(Hauteur, Largeur, Conditions),
% 13 X 13 --> 1 219 359 inférences, 0.27 CPU
% grille12(Hauteur, Largeur, Conditions),
% 17 X 17 force 6 --> 10 549 305 inférences, 2.30 CPU
% grille31(Hauteur, Largeur, Conditions),
% 17 X 17 force 8 --> 17 544 232 inférences, 3.73 CPU
% grille30(Hauteur, Largeur, Conditions),
% 17 X 17 force 8 --> 2 153 462 037 inférences, 445.28 CPU
grille43(Hauteur, Largeur, Conditions),
% 17 X 17 force 8 --> 157 326 579 inférences, 33.89 CPU
% la même qsue la précédente mais la liste des contraintes est inversée
% grille43b(Hauteur, Largeur, Conditions),
Len is Hauteur * Largeur,
length(Soluce, Len),
% les cases ont deux valeurs possibles
% noires -> 0
% blanches -> 1
Soluce ins 0..1,
% pour avoir des statistiques sur la résolution
time(kuromasu(Hauteur, Largeur, Conditions, Soluce, ff)),
affiche_kuromasu(Hauteur, Largeur, Soluce).Un exemple de définition de contraintes est donné ici :
grille96(13, 13, Conditions) :-
Conditions = [case( 0, 2, 3),
case( 0, 6, 6),
case( 0, 8, 8),
case( 0, 10, 4),
.....VI. La recherche des contraintes à partir d'une grille▲
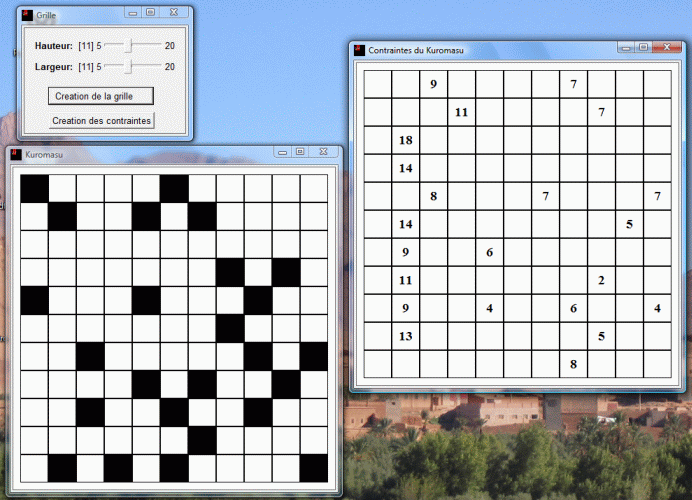
Ce programme est muni d'une interface XPCE qui permet la saisie de la grille par simple clic sur les cases à noircir.
La partie intéressante est la création des contraintes à partir de la grille, elle est effectuée par la règle cree_toutes_les_contraintes/6.
La méthode proposée ici pour la création des contraintes peut être améliorée, libre au lecteur d'approfondir la question. Le seul but de cette partie est de montrer que c'est possible, pas de proposer une création de contraintes conduisant à une résolution difficile de la grille. Il est même possible que la création de la liste des contraintes échoue pour certaines grilles particulières.
La méthode choisie lit la grille ligne par ligne. On force une contrainte pour toute suite d'au moins deux cases blanches. Pour compliquer tout de même un peu, on impose que la case numérotée ne soit pas sur la première. Le prédicat s'écrit cree_contrainte(NumLigne, Max, Ligne, N, Prev, CondCour, CondFin).
- NumLigne : le numéro de la ligne étudiée ;
- Max : le maximum de cases visibles pour une case de la grille (Largeur + Hauteur – 1) ;
- Ligne : la liste des valeurs de la ligne restant à étudier ;
- N : le numéro courant de la case étudiée ;
- Prev : le numéro de début de séquence de cases blanche en cours ;
- CondCour : la liste des contraintes déjà créées ;
- ContFin : la liste finale des contraintes.
% C'est la fin de la ligne,
% on cree la dernière contrainte
cree_contrainte(Ligne, Max, [], N, Prev, CondCour, CondFin) :-
( Prev = -1, Deb = 0
;
Deb = Prev
),
N1 is N - 1,
( Deb < N1 ,
Deb1 is Deb + 1,
Colonne in Deb1 .. N1,
Nb in 2 .. Max,
append(CondCour, [case(Ligne, Colonne, Nb)], CondFin)
;
CondFin = CondCour
).
% On rencontre une case noire
% on cree la contrainte
cree_contrainte(Ligne, Max, [0 | T], N, Prev, CondCour, CondFin) :-
( Prev = -1, Deb = 0
;
Deb = Prev
),
N1 is N - 1,
( Deb < N1 ,
Deb1 is Deb + 1,
Colonne in Deb1 .. N1,
Nb in 2 .. Max,
append(CondCour, [case(Ligne, Colonne, Nb)], NewCond)
;
NewCond = CondCour
),
NewDeb is N+1,
cree_contrainte(Ligne, Max, T, NewDeb, NewDeb, NewCond, CondFin).
% on rencontre une case blanche on continue
cree_contrainte(Ligne, Max, [1 | T], N, Deb, CondCour, CondFin) :-
N1 is N+1,
cree_contrainte(Ligne, Max, T, N1, Deb, CondCour, CondFin).On voit ici le résultat obtenu pour la grille exemple.
VII. Conclusion Liens sur le Kuromasu▲
On voit ici l'intérêt de la bibliothèque de contraintes de Prolog. Il n'y a pas besoin de chercher une stratégie compliquée (je n'ai jamais résolu un Kuromasu à la main !), il n'y a pas de cas particuliers à traiter, on se contente de traduire les règles en calculs, à imposer des valeurs pour les résultats de ces calculs et on lance la résolution.
La résolution du Kuromasu proposé dans l'exemple se fait sur ma machine (processeur Intel Core 2, 1,86 GHz, Vista Édition Intégrale) en 3,4 secondes. Le programme a été testé sous Linux Open-Suse.
D'autres Kuromasu sont proposés ici. La grille 17 X 17 numéro 31 force 6, est résolue en 2,3 secondes, la numéro 30, force 8, est résolue en 3,7 secondes, enfin la plus difficile la numéro 43 en 445,3 secondes soit tout de même plus de 7 minutes !
Il faut remarquer que l'ordre dans lequel la liste des contraintes est donnée est important pour la rapidité de la recherche : si on inverse la liste des contraintes de la grille 43, la durée de la recherche de la solution tombe à 34,2 secondes ! Une image de la grille initiale permet de le comprendre.
On voit que sur la dernière ligne, deux cases consécutives sont numérotées, dont l'une à 2. Cela force trois cases noires : celle à gauche de 5, et les cases au-dessus et à droite de 2. Il est préférable d'imposer cette obligation dès le début plutôt qu'à la fin de la résolution ! C'est le seul cas où la pratique de la résolution des Kuromasu sert à quelque chose dans ce programme !
Un exemple d'algorithme de résolution est détaillé ici. Une étude plus approfondie des méthodes de résolution est donnée ici.
VIII. Le code complet du programme▲
Il y a trois programmes fournis :
- un programme de type console pour tester la création des grilles à partir de listes de contraintes créées à la main. Le fichier principal est « solve-console.pl » et la commande est solve_console ;
- un programme interactif écrit en XPCE pour tester la création des grilles à partir de contraintes écrites directement dans les cases. Le fichier principal est « solve-XPCE.pl » et la commande est solve_XPCE ;
- un programme interactif écrit en XPCE pour la création de la liste de contraintes à partir de la grille. Le fichier principal est « genere-Kuromasu.pl » et la commande est genere.
Le zip des fichiers est accessible ici. Le pdf de l'article est accessible ici.
IX. Visualisation de la création de la grille▲
Il est possible à l'aide d'une modification du code de visualiser le travail effectué par Prolog au moment de la création des contraintes. La visualisation a été effectuée sur la grille 9 X 9 la plus rapide. Un lecteur patient peut faire le test sur la grille 17 X 17 numéro 43.
Cliquer iciAnimation du Kuromasu pour voir l'animation.
Cliquer iciLe source pour visualiser la création de la grille pour obtenir le source permettant la visualisation.
X. Les options de labeling pour la recherche de solutions▲
Toutes les options de labeling se trouvent sur cette pageLes options de labeling. Elles ont pour but d'orienter la stratégie de recherche en modifiant l'ordre d'affectation des valeurs aux différentes variables affectées aux contraintes.
Les différents types d'options pour le labeling
- Les options qui contrôlent l'ordre dans lequel les variables sont instanciées : leftmost, min, max, ff, ffc.
- Les options qui concernent les choix d'instanciation d'une variable donnée par rapport à son domaine : up, down.
- Les options qui spécifient la manière dont sont instanciées les variables : step, enum, bisect.
- Enfin l'ordre des solutions peut être influencé par les options min(Expr) et max(Expr) ou Expr est une expression mathématique.
Les options par défaut sont leftmost, up et step : les variables sont examinées dans l'ordre de leur apparition dans la déclaration des contraintes (leftmost), chaque variable est instanciée de la plus petite à la plus grande valeur possible (up), un choix binaire est fait entre « la variable prend la valeur V » ou « la variable ne prend pas la valeur V » (step); cette option se comprend mieux si on considère l'option enum où là, un choix multiple est fait entre les différentes valeurs du domaine de la variable : la variable prend la valeur V1, ou la variable prend la valeur V2 ou la variable prend la valeur V3…
Certaines options ont un effet très spectaculaire sur la rapidité de recherches.
X-A. L'option « ff »▲
Avec cette option, la variable la plus à gauche ayant le plus petit domaine de valeurs est examinée en premier pour détecter les échecs le plus rapidement possible, l'arbre de recherche est ainsi fortement réduit. C'est souvent une bonne stratégie pour obtenir rapidement le bon résultat.
Un exemple parlant est obtenu avec le problème des n_reines écrit par Markus TriskaLa home page de Markus Triska.
:- use_module(library(clpfd)).
n_queens(N, Qs) :-
length(Qs, N),
Qs ins 1..N,
safe_queens(Qs).
safe_queens([]).
safe_queens([Q|Qs]) :- safe_queens(Qs, Q, 1), safe_queens(Qs).
safe_queens([], _, _).
safe_queens([Q|Qs], Q0, D0) :-
Q0 #\= Q,
abs(Q0 - Q) #\= D0,
D1 #= D0 + 1,
safe_queens(Qs, Q0, D1).On remarquera que la phase de labeling n'est pas dans le code.
On lance une recherche pour un échiquier de 80 cases de largeur !
?- n_queens(80, Qs), time(labeling([], Qs)).
Action (h for help) ? abort
% 8,237,652 inferences, 1.510 CPU in 4.564 seconds (33% CPU, 5455399 Lips)
Execution AbortedOn peut laisser tourner le programme très longtemps.
Donnons maintenant l'option « ff » :
?- n_queens(80, Qs), time(labeling([ff], Qs)).
% 714,139 inferences, 0.150 CPU in 0.430 seconds (35% CPU, 4760927 Lips)
Qs = [1, 3, 5, 44, 42, 4, 50, 7, 68|...].Le résultat est obtenu en moins d'une demi-seconde !
Malheureusement, cette option n'est guère utile pour la résolution des Kuromasu les cases n'ayant que deux valeurs possibles 0 et 1.
L'option « ffc » ressemble beaucoup à l'option « ff ». La variable la plus à gauche ayant le plus petit domaine de valeurs et intervenant dans le plus de contraintes est sélectionnée.
X-B. L'option « bisect »▲
Avec cette option, l'affectation des valeurs aux variables est faite en partant du milieu de l'intervalle des valeurs possibles.
On a une idée de l'utilité de cette option avec la résolution du problème 7-11Le problème 7-11.
?- time((Vs=[A,B,C,D], Vs ins 0..sup, sum(Vs,#=,711), A*B*C*D#=711000000, chain(Vs, #>=), labeling([ff], Vs))).
% 2,934,328 inferences, 1.703 CPU in 1.695 seconds (100% CPU, 1722908 Lips)
Vs = [316, 150, 125, 120],
A = 316,
B = 150,
C = 125,
D = 120.
?- time((Vs=[A,B,C,D], Vs ins 0..sup, sum(Vs,#=,711), A*B*C*D#=711000000, chain(Vs, #>=), labeling([ff,bisect], Vs))).
% 1,559,185 inferences, 0.641 CPU in 0.642 seconds (100% CPU, 2433850 Lips)
Vs = [316, 150, 125, 120],
A = 316,
B = 150,
C = 125,
D = 120.Le nombre d'inférences est divisé par 2 et le temps de recherche par 3.
Les nombres obtenus doivent être divisés par 100 pour être les solutions du problème 7-11.
XI. Remerciements▲
Je tiens à remercier particulièrement Markus TriskaLa home page de Markus Triska pour ses conseils sur l'utilisation de la bibliothèque de contraintes et ses remarques tout au long de l'élaboration de cet article, SpiceGuid pour sa relecture de l'article et ses remarques constructives et enfin Bérénice MAURELProfil de Bérénice MAUREL et Wachter pour leur relecture finale de l'article.